Relaxing Ocean Simulation 🌊

Build Demo

This project is a GPU-driven ocean simulation that combines FFT wave generation, interactive ripples via iWave, and GPU buoyancy. The goal was to move beyond simple Gerstner waves and build a scalable, realistic, yet interactive ocean surface suitable for games.

FFT Waves

My first attempt at ocean simulation was with Gerstner waves for a student game (DuoQ). While functional, the results ended up looking pretty simplistic and cartoonish. I wanted more realism and extensibility.

Inspired by The Technical Art of Sea of Thieves, I explored using Fast Fourier Transform (FFT) waves. The core idea is to generate wave information in the frequency (spectrum) domain and transform it into the spatial domain using the Inverse FFT (Cooley–Tukey algorithm).

I used the Phillips spectrum to define the statistical distribution of wave heights given various parameters such as gravity, wind direction, choppiness, and amplitude. From this, I generated two key textures that will later go through iFFT compute shaders to extract spatial information:

• Displacement Map – encodes vertical and horizontal wave displacement.
• Normal Map – encodes surface orientation for light shading.

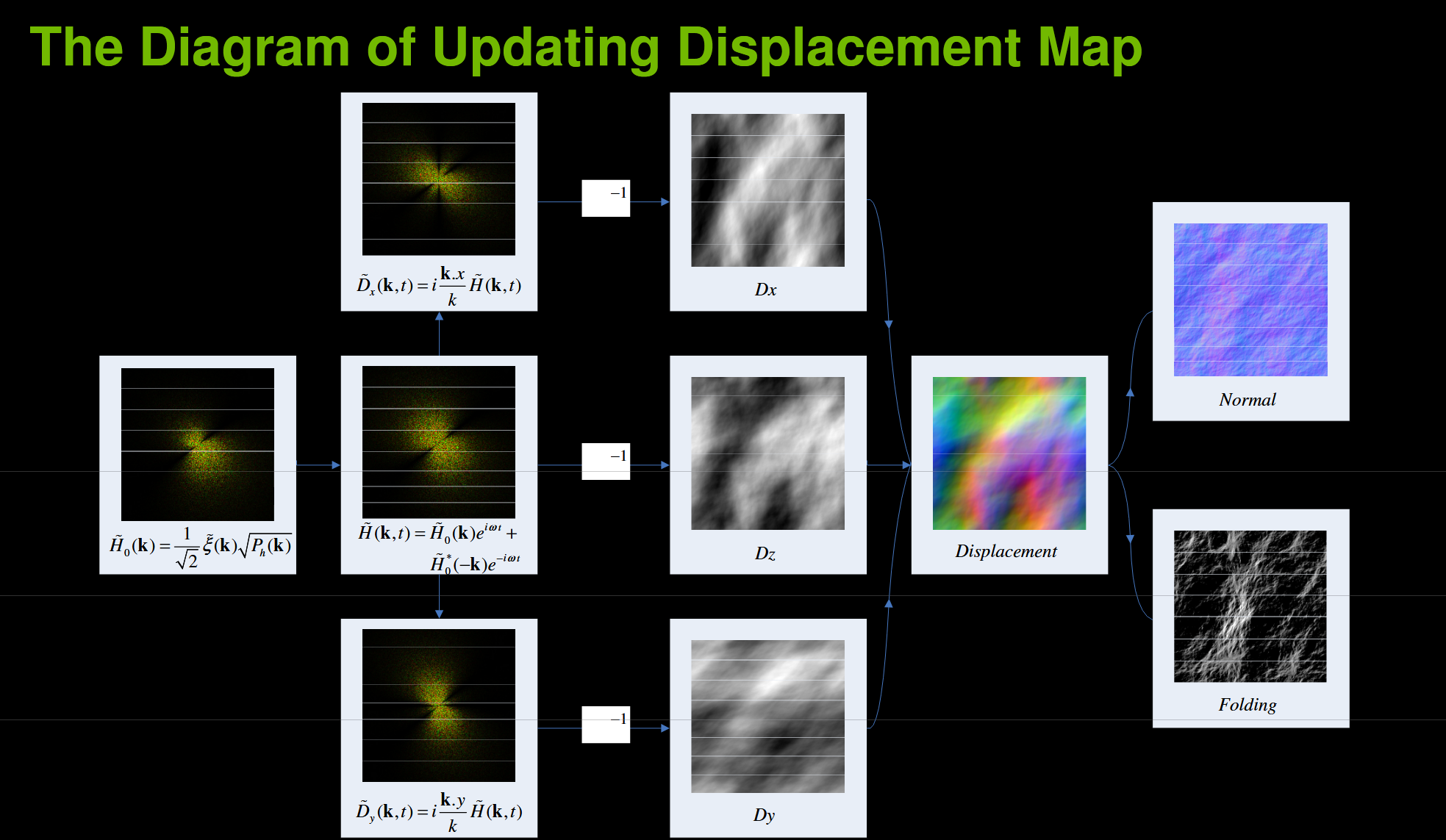
For further visual realism, I implemented foam generation by running a Jacobian test on the displacement map that could identify regions where waves fold or intersect - here, foam buildup would naturally happen. This produced breaking wave crests and dynamic foam patterns.

// https://people.computing.clemson.edu/~jtessen/reports/papers_files/coursenotes2004.pdf
float jxx = 1 + lambda * dx_dx;
float jyy = 1 + lambda * dy_dy;
float jxy = lambda * dx_dy;
float jyx = lambda * dy_dx;
float negativeJ = 0.5f * (jxx + jyy) - 0.5f * sqrt((jxx - jyy) * (jxx - jyy) + 4.0f * jxy * jxy);
float foam = saturate(1.0f - negativeJ);
foam = smoothstep(0.3f, 1.0f, foam); // Smooth the transition for foam effect

Interactive Ripples (iWave)

To make the ocean reactive to objects, I integrated the iWave algorithm for local water interactions.

I placed a camera above the ocean plane that captures silhouettes of objects intersecting or hovering above the water. This data is written into a render texture, which serves as the input to the iWave simulation.

The iWave algorithm applies a convolution kernel to simulate ripple propagation outward from disturbance sources. The resulting ripple texture is sampled in the shader and blended with the FFT surface normals, allowing characters, boats, or other objects to leave trails and ripples in the water.

// iWave set up - the key part
m_convolutionKernel = new float[(2 * m_kernelSize + 1) * (2 * m_kernelSize + 1)];

float g0 = 0.0f;
for (int n = 0; n < m_iterations; n++)
{
	float qn = m_deltaQ * n;
	g0 += qn * qn * Mathf.Exp(-m_sigma * qn * qn);
}

for (int k = -m_kernelSize; k <= m_kernelSize; k++)
{
	for (int l = -m_kernelSize; l <= m_kernelSize; l++)
	{
		// idx = x * size + y
		float r = Mathf.Sqrt((float)(k * k + l * l));
		float val = 0.0f;
		for (int n = 0; n < m_iterations; n++)
		{
			float qn = m_deltaQ * n;
			val += qn * qn * Mathf.Exp(-m_sigma * qn * qn) * (float)j0(qn * r);
		}
		SetKernelValue(k, l, val / g0);
	}
}

GPU Buoyancy

Objects floating on the water surface are displaced directly on GPU using the FFT displacement map. This ensures that buoyant objects ride the same waves visible in the rendering, keeping the physics and visuals in sync without extra CPU-side calculations.

// vertex shader
void vert (inout appdata_full v)
{
	UNITY_SETUP_INSTANCE_ID(v); // Setup instance ID

	float4 center = mul(unity_ObjectToWorld, float4(0, 0, 0, 1));
	float buoyancyStrength = UNITY_ACCESS_INSTANCED_PROP(Props, _BuoyancyStrength);
	float2 uv = center.xz / _MeshSize;
	uv += 0.5f;
	float3 disp = tex2Dlod(_DisplacementTex, float4(uv, 0, 0)).xyz;
	v.vertex.xyz += disp * buoyancyStrength;
}

Rendering

The shading model is built on a Phong lighting model enhanced with a Fresnel term. The Fresnel effect blends between diffuse ocean color and reflected sky color, giving the water its characteristic reflective look.

Normals are combined from two sources:

1. FFT normals for large-scale ocean motion.
2. iWave ripple normals for fine local interactions.

Foam textures are blended on top, guided by the Jacobian test results and displacement intensity. This produces convincing shoreline foam and cresting waves.

A core section of the shader blends the FFT normals with iWave ripple normals before applying lighting:

// sample ripple texture (convert world pos to UV)
float2 uv = i.worldVertex.xz / _MeshSize + 0.5f;

float hL = tex2D(_RippleTex, uv + float2(-texel.x, 0)).r;
float hR = tex2D(_RippleTex, uv + float2(texel.x, 0)).r;
float hD = tex2D(_RippleTex, uv + float2(0, -texel.y)).r;
float hU = tex2D(_RippleTex, uv + float2(0, texel.y)).r;

// compute ripple normals
float dx = (hDL + 2.0 * hL + hUL) - (hDR + 2.0 * hR + hUR);
float dy = (hDL + 2.0 * hD + hDR) - (hUL + 2.0 * hU + hUR);
float3 n1 = normalize(float3(dx, dy, 1.0f / _NormalStrength));

// combine with FFT normal
float3 n2 = tex2D(_NormalTex, i.uv).rgb * 2.0f - 1.0f;
float3 r = normalize(float3(n1.xy + n2.xy, n1.z * n2.z));

// final world normal
float3 worldNormal = UnityObjectToWorldNormal(r);

// Fresnel + foam shading
float reflectivity = pow(1.0f - saturate(dot(viewDirection, worldNormal)), _FresnelPower);
_DiffuseColor = lerp(_SkyColor, _DiffuseColor, reflectivity);

float foam = tex2D(_FoamTex, i.uv).r;

This combination of FFT, iWave, Fresnel, and foam creates a water surface that’s not just realistic but also interactive and dynamic.

Further exploration

• eWave instead of iWave
• Other spectrum aside from Phillips
• Physically accurate buoyancy
• Optimization for scaling bigger oceans
• Boids simulation of seagulls